987. Гвозди

На прямой доске вбиты гвозди. Любые два гвоздя можно соединить ниткой. Требуется соединить некоторые пары гвоздей ниткой так, чтобы к каждому гвоздю была привязана хотя бы одна нитка, а суммарная длина всех нитей была бы минимальна.

Вход. В первой строке записано количество гвоздей n (1 ≤ n ≤ 100). В следующей строке записано n чисел – координаты всех гвоздей (неотрицательные целые числа, не превосходящие 10000).

Выход. Вывести минимальную суммарную длину всех нитей.

Пример входа	Пример выхода
5 4 10 0 12 2	6

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Отсортируем координаты гвоздей в массиве а. Пусть dp[i] равно минимальной суммарной длине всех нитей, когда любые два гвоздя от первого (нумерация гвоздей начинается с 1) до i-го соединены нитью.

При n = 2 оба гвоздя обязательно должны быть соединены нитью:

dp[2] = a₂ – a₁

При n = 3 следует соединить первый гвоздь со вторым, а второй с третьим. Таким образом

dp[3] = a₃ – a₁

При добавлении i-го гвоздя имеются две возможности присоединения его нитью:

1) соединяем первые i – 2 гвоздей между собой, а (i – 1)-ый гвоздь соединяем с i-ым. Общая длина нити для такого соединения составит dp[i – 2] + a[i] – a[i – 1].

2) соединяем первые i – 1 гвоздей между собой, а i-ый гвоздь подсоединяем к (i – 1)-ому. Нам потребуется dp[i – 1] + a[i] – a[i – 1] нити.

Выбираем тот метод соединения, при котором общая длина нити наименьшая. То есть

dp[i] = min(dp[i – 2], dp[i – 1]) + a[i] – a[i – 1]

Пример

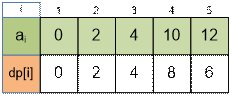
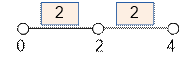
Отсортируем координаты гвоздиков для заданного примера: 0, 2, 4, 10, 12. Для двух гвоздей dp[2] = 2 – 0 = 2. Для трех гвоздей нитью следует соединять их все (к каждому гвоздю должна быть привязана хотя бы одна нить), поэтому

dp[3] = (4 – 2) + (2 – 0) = 4

Вычислим оптимальную длину нити для 4 гвоздей:

dp[4] = min(dp[2], dp[3]) + 10 – 4 = 2 + 6 = 8

Для 5 гвоздей наименьшая возможная длина нити составит

dp[5] = min(dp[3], dp[4]) + 12 – 10 = 4 + 2 = 6

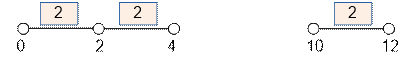
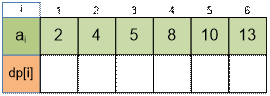
Упражнение

Вычислите значения dp[i] для следующих входных данных:

Реализация алгоритма

В массиве а храним координаты гвоздей. Объявим также массив результатов dp.

#define MAX 101

int a[MAX], dp[MAX];

Читаем входные данные.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Отсортируем координаты гвоздей.

sort(a+1,a+n+1);

Инициализируем dp[2] и dp[3].

dp[2] = a[2] - a[1];

dp[3] = a[3] - a[1];

Пересчитываем ячейки массива dp по формуле.

for(i = 4; i <= n; i++)

dp[i] = min(dp[i-1],dp[i-2]) + a[i] - a[i-1];

Выводим ответ.

printf("%d\n",dp[n]);

Java реализация

import java.util.*;

class Main

{

static int a[] = new int[101];

static int dp[] = new int[101];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

for (int i = 1; i <= n; i++)

a[i] = con.nextInt();

Arrays.sort(a,1,n+1);

dp[2] = a[2] - a[1];

dp[3] = a[3] - a[1];

for(int i = 4; i <= n; i++)

dp[i] = Math.min(dp[i-1],dp[i-2]) + a[i] - a[i-1];

System.out.println(dp[n]);

con.close();

}

}